Estimation de la distance au Soleil de Neptune

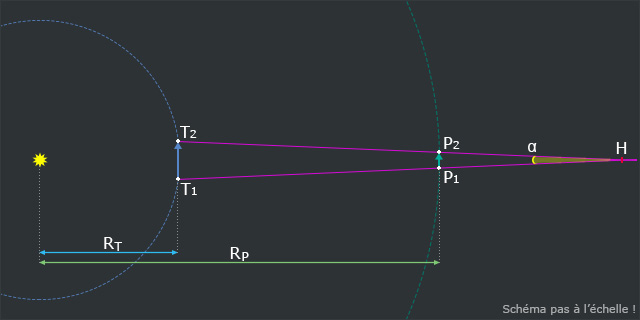
Une planète supérieure, située au-delà de l’orbite de la Terre, est en opposition lorsque le Soleil, la Terre et cette planète sont alignés : elle nous est alors visible dans la direction opposée à celle du Soleil.

Deux photographies d’une planète proche de l’opposition réalisées à quelques jours d’intervalle permettent d’observer son mouvement apparent sur la voute céleste, à un moment où le déplacement des planètes peut être ramené à deux segments parallèles. La mesure de l’angle de déplacement apparent permet alors d’estimer la distance de cette planète au Soleil, en ne connaissant préalablement que la distance Terre-Soleil, la durée de l’année, et la valeur de la constante gravitationnelle.

Acquisition, traitement et analyse des images

J’ai profité de l’opposition de Neptune (aucun rapport avec l’astrologie) du 5 septembre 2017 pour faire cette mesure à l’Observatoire du Planétarium de Vaulx-en-Velin.

J’ai observé Neptune les soirs des 4 et 6 septembre 2017, en utilisant le télescope AstroSib RC360 (2880mm de focale théorique) et la caméra CCD Atik 460ex, qui a un capteur avec 2750×2200 photosites distants de 4,54μm, pour réaliser des séries de 10 images chaque soir. J’ai notamment pris soin de ne pas saturer l’image de la planète (magnitude 8).

Une mesure astrométrique des clichés a été utilisée lors des acquisitions (avec Astrometry.net) pour déterminer la longueur focale réelle du montage optique : 2960mm.

Les images ont été prétraitées, alignées, et analysées pour déterminer les meilleures (sélectionnées par la FWHM des étoiles) de chaque soirée. Pour les deux lots, les 3 meilleures images consécutives sont assemblées, les heures des images médianes servent à dater les mesures : 04/09 à 22:32:28 et 06/09 à 21:15:43, soit 168 195 secondes d’écart.

Ces deux images ont à leur tour été alignées et superposées :

Triton est le plus gros satellite de Neptune, sa période de révolution rapide (5j 21h) est bien mise en évidence. L’étoile la plus brillante du champ est TYC 5813-80-1.

La position des centroïdes des deux images de Neptune sur cette photo composite a été déterminée au centième de pixel près, permettant de calculer un écart de 610,70 pixels.

Calculs

Notations et valeurs connues :

La planète en opposition est observée à deux moments d’écart Δt. Pendant cette durée elle avance sur l’arc P₁P₂ et la Terre (qui se déplace plus vite) sur l’arc T₁T₂. Δt étant petit par rapport aux périodes des planètes et celles-ci étant proches d’êtres alignées avec le Soleil, je fais une approximation de ces arcs en deux segments parallèles. Le Soleil, T₁ et P₁ sont considérés alignés.

Je note α l’angle du mouvement apparent de la planète, vue depuis la Terre, en la durée Δt ; R_T la distance Soleil-Terre (1 unité astronomique, 149,6 millions de km), R_P la distance Soleil-planète, que je cherche ; V_T la vitesse orbitale de la Terre, V_P la vitesse de la planète (leurs orbites sont ramenées à des cercles, leurs masses sont négligeables face à celle du Soleil) ; M_S la masse du Soleil, G la constante gravitationnelle (6,674×10^-11 N×m²/kg²), P_T la période de révolution de la Terre (365,24 jours).

Calcul de l’angle de déplacement apparent α :

Avec P la distance entre les centres des photosites (4,54×10^-6m), F la longueur focale du télescope (2,960m) :

$\mathrm{Échantillonnage} = \arctan \left(\frac{\mathrm{P}}{\mathrm{F}}\right) \approx 1,534\times {10}^{–6} \mathrm{rad}/\mathrm{px}$

L’angle du mouvement apparent est

$\mathrm{\alpha }=610,70\times \arctan \left(\frac{\mathrm{P}}{\mathrm{F}}\right)\approx 9,367\times {10}^{–4} \mathrm{rad}$

ou

$\mathrm{\alpha }=610,70\times \arctan \left(\frac{\mathrm{P}}{\mathrm{F}}\right)\times \frac{180\times 3600}{\mathrm{\pi }}\approx 193,2 \mathrm{arcsec}$

Calculs de la masse du Soleil M_S et de la vitesse orbitale de la Terre V_T :

D’après les lois de Kepler et de Newton :

$\frac{{{\mathrm{P}}_{\mathrm{T}}}^2}{{{\mathrm{R}}_{\mathrm{T}}}^3}=\frac{4\mathrm{\pi }²}{\mathrm{G}\times {\mathrm{M}}_{\mathrm{S}}} \to {\mathrm{M}}_{\mathrm{S}} = \frac{4\mathrm{\pi }²\times {{\mathrm{R}}_{\mathrm{T}}}^3}{\mathrm{G}\times {\mathrm{P}}_{\mathrm{T}}²}\approx 1,989\times {10}^{30} \mathrm{kg}$

${\mathrm{V}}_{\mathrm{T}} = \sqrt{\frac{\mathrm{G}\times {\mathrm{M}}_{\mathrm{s}}}{{\mathrm{R}}_{\mathrm{T}}}}\approx 29 786 \mathrm{m}/\mathrm{s}$

Calcul de R_P, distance de la planète au Soleil :

Je considère que

$\mathbf{\alpha }\mathbf{=}\frac{||{\mathbf{P}}_{\mathbf{1}}{\mathbf{P}}_{\mathbf{2}}||}{||{\mathbf{P}}_{\mathbf{1}}\mathbf{H}||}\mathbf{=}\frac{||{\mathbf{T}}_{\mathbf{1}}{\mathbf{T}}_{\mathbf{2}}||}{||{\mathbf{P}}_{\mathbf{1}}\mathbf{H}||\mathbf{+}||{\mathbf{T}}_{\mathbf{1}}{\mathbf{P}}_{\mathbf{1}}||}$

||P₁H|| étant inconnu, il doit être remplacé dans cette égalité. J’utilise pour cela :

$||{\mathrm{T}}_1{\mathrm{P}}_1|| = {\mathrm{R}}_{\mathrm{P}}–{\mathrm{R}}_{\mathrm{T}} ,$

$||{\mathrm{P}}_1{\mathrm{P}}_2||={\mathrm{V}}_{\mathrm{P}}\times \mathrm{\Delta t} \mathrm{et} ||{\mathrm{T}}_1{\mathrm{T}}_2||={\mathrm{V}}_{\mathrm{P}}\times \mathrm{\Delta t} ,$

${\mathrm{M}}_{\mathrm{S}} = \frac{4\mathrm{\pi }²\times {{\mathrm{R}}_{\mathrm{T}}}^3}{\mathrm{G}\times {\mathrm{P}}_{\mathrm{T}}²} ,$

${\mathrm{V}}_{\mathrm{P}} = \sqrt{\frac{\mathrm{G}\times {\mathrm{M}}_{\mathrm{s}}}{{\mathrm{R}}_{\mathrm{P}}}} \mathrm{et} {\mathrm{V}}_{\mathrm{T}} = \sqrt{\frac{\mathrm{G}\times {\mathrm{M}}_{\mathrm{s}}}{{\mathrm{R}}_{\mathrm{T}}}}$

Avec ces égalités :

$\mathrm{\alpha }=\frac{||{\mathrm{P}}_1{\mathrm{P}}_2||}{||{\mathrm{P}}_1\mathrm{H}||} \to ||{\mathrm{P}}_1\mathrm{H}|| = \frac{||{\mathrm{P}}_1{\mathrm{P}}_2||}{\mathrm{\alpha }}=\frac{1}{\mathrm{\alpha }}\times {\mathrm{V}}_{\mathrm{P}}\times \mathrm{\Delta t} = \frac{\mathbf{\Delta t}}{\mathbf{\alpha }}\sqrt{\frac{\mathbf{G}\mathbf{\times }{\mathbf{M}}_{\mathbf{S}}}{{\mathbf{R}}_{\mathbf{P}}}}$

et

$\mathrm{\alpha }=\frac{||{\mathrm{T}}_1{\mathrm{T}}_2||}{||{\mathrm{P}}_1\mathrm{H}||+||{\mathrm{T}}_1{\mathrm{P}}_1||} \to ||{\mathrm{P}}_1\mathrm{H}|| = \frac{||{\mathrm{T}}_1–{\mathrm{T}}_2||}{\mathrm{\alpha }}–||{\mathrm{T}}_1{\mathrm{P}}_1|| = \frac{\mathbf{\Delta t}}{\mathbf{\alpha }}\mathbf{\times }{\mathbf{V}}_{\mathbf{T}}\mathbf{–}\mathbf{(}{\mathbf{R}}_{\mathbf{P}}\mathbf{–}{\mathbf{R}}_{\mathbf{T}}\mathbf{)}$

J’obtiens donc :

$\frac{\Delta \mathrm{t}}{\mathrm{\alpha }}\sqrt[]{\frac{\mathrm{G}\times {\mathrm{M}}_{\mathrm{S}}}{{\mathrm{R}}_{\mathrm{P}}}}=\frac{\Delta \mathrm{t}}{\mathrm{\alpha }}\times {\mathrm{V}}_{\mathrm{T}}–\left({\mathrm{R}}_{\mathrm{P}}–{\mathrm{R}}_{\mathrm{T}}\right) \to \sqrt[]{\frac{\mathbf{G}\mathbf{\times }{\mathbf{M}}_{\mathbf{S}}}{{\mathbf{R}}_{\mathbf{P}}}}\mathbf{+}\frac{\mathbf{\alpha }}{\mathbf{\Delta t}}\mathbf{\times }\mathbf{(}{\mathbf{R}}_{\mathbf{P}}\mathbf{–}{\mathbf{R}}_{\mathbf{T}}\mathbf{)}\mathbf{–}{\mathbf{V}}_{\mathbf{T}}\mathbf{=}\mathbf{0}$

R_P est alors la seule inconnue de cette équation, et c’est justement ce que je cherche !

Résolution de l’équation :

Ne pouvant pas résoudre aisément l’équation, j’utilise un tableur pour trouver la valeur de R_P qui l’annule, par essais successifs. Les seules valeurs saisies sont celles liées à l’observation, la constante gravitationnelle G, la longueur de l’unité astronomique R_T et la durée de l’année P_T.

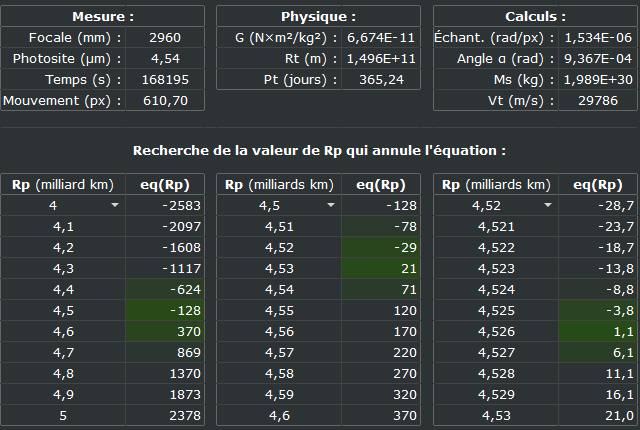
Je peux alors estimer la distance de Neptune au Soleil à 4,526 milliards de kilomètres.

Le demi grand-axe de son orbite est 4,503 milliards de km, l’estimation est 0,5% au-dessus. Le logiciel Stellarium indique qu’à cette date la planète géante était en réalité à 4,480 milliards de km du Soleil, la Terre en était à 150,8 millions de km.

Cette observation est inspirée de celle de Philippe Boeuf (opposition de Neptune du 17 août 2009).